今回から、実際の過去問題や令和6年の問題を例にして、測量士補試験の計算問題を解いていこうと思います。
数学アレルギーの人でも、式の見た目で「うへぇ~」とならないよう落ち着いて、先に覚えるものを早めに覚えてしまって、実際に手を動かしていたら、自然と数学アレルギーも薄くなっていくと思います。あと、記号の意味を知ってしまえば、そう難しいことを言っていたわけではないんだなと判ってきます。
この測量士補試験の基本的課題は、四則計算をいかに手計算で間違えないかになります。これ案外、間違うんですよね。
普通の引き算の計算では、足らないときは、左隣りから10を借りてきますよね。角度の場合は、60を借りてくるのですが、漫然と手計算していたらよく間違えてしまいます。
あと、このブログの解き方以外に、テキストやYouTubeの番組などによって、解き方が違うと思います。
試験当日の回答があっていればいいのですから、ご自分のやりやすい、納得できる解き方を探してくださいね。
令和6年 測量士補試験 No.3 法規の中の基礎数学 ラジアンと正弦定理
測量法という法律が文章問題のメインになるのですが、それに抱き合わせる形で、初っ端の計算問題として、「測量の基礎数学」の問題が出ます。
法規の中なのに、計算問題が出てくるとはなにごと?って思いましたが、まぁ、試験当局の意図なので仕方がありません。
例年、問題No.3が当てはまります。
平成29年から令和3年まで同じような問題でした。内容は、ラジアンという角度を使った問題と、三角形の辺の長さをサインやコサインを使って求める問題です。
そして、令和4年と令和5年は、問題の毛色が変わって、「測量の誤差」と言う問題が出ました。
本年度、令和6年は、また基礎の数学になっていました。
来年、どちらが出るのかは、わかりませんので、両方見ておきたいと思います。まずは、基礎数学からになります。

国土地理院HPから引用
aのラジアンの問題
まず、ラジアンとは何ぞやなのですが、円の半径と、その円の円弧の長さが同じになるときの角度のことです。1ラジアン57.3°と決まっています。これは、円の大小は関係なくて、どんなに大きい円でも、1ラジアン57.3°、又は、206265”秒になります。こちらのYouTube番組でラジアンを優しく解説されています。
で、問題aの選択肢を見ると、解答の数字の幅が広いですよね。
多少の計算の誤差の範囲なら、簡略化した計算で、この問題の選択肢を選ぶことが出来ると、私は判断しました。小数点以下の多い手計算が面倒臭いのと間違いの元だからです。
で、比例計算で、aを説いていきます。
1ラジアンのとき、57.3°なのですから、84°…のときは、何ラジアンか?
時間と手間の短縮で84°以下は省略して計算しました。
1:57.3=x:84
これを解くと、x=84÷57.3=1.465≒1.47ラジアン となります。
☆この問題をきちんと解くなら、84°15’36”を一度、全部、秒”に戻してやります。
角度は時計と同じ60進法なので、ちょっと計算します。
84°には3600をかけて、302400”
15’には60をかけて、900”
36”はそのまま
これらを足すと、303336”秒となりますね。
で、これをまた比例計算でやるのです。
1ラジアンは206265”秒ですので、
1:206265=x:303336
x=303336÷206265≒1.470 となります。
°を秒に直すなら×3600 ’を秒に直すなら×60
逆に、”を°に直すなら÷3600 ’を°に直すなら÷60 となります
これは、他の過去問を解く上で必要な知識ですので、暗記しておきましょう
因みに、84°15’36”を、全部°度に直すことも出来ます。
15’÷60=0.25 36”÷3600=0.01 これらと84°を足して、84.26°として計算してもOKです。
bの問題(正弦定理を使って)
まず、この三角形の長さを出す問題で図がないなら、作ってみましょう。
∠Cが70°、∠Bが30°なら、残りの∠Aは、80°ですよね。
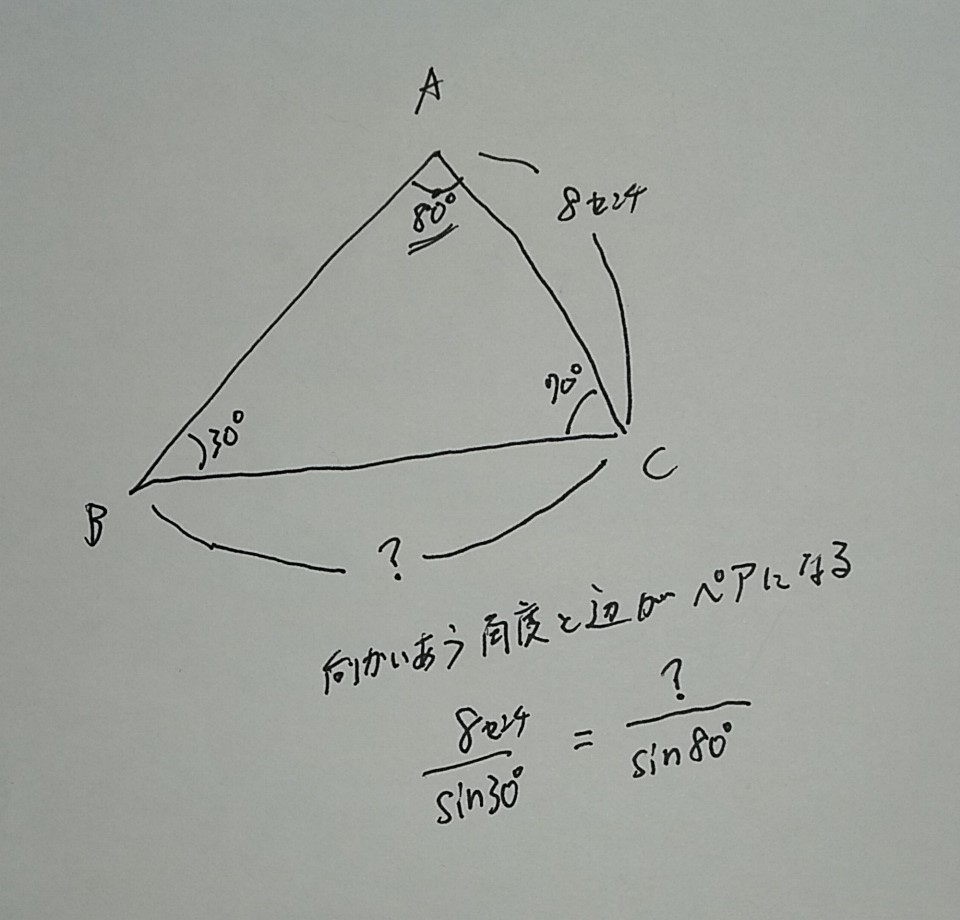
でここで、正弦定理というものを使います。サインのやつですね。
三角形で、ある角度と向かい合った辺の長さのペアを使うのです。
正弦定理の解説はこちら
この公式は覚えるしかないんですが、正弦定理は、文系の人でも理屈抜きでも覚えやすいものだと思います。難しそうな名前にビビッてしまうのですけどw
そして、8/sin30°=x/sin80° となります。
たすき掛けで、掛けてあげると、
sin30 × X = sin80 × 8
sinは、問題用紙の後ろに、関数表という数字の一覧がありますので、これから引っ張ってきます。
そうすると、
x=8÷0.5×0.98481=15.75…≒15.8m となります。
a,bの答えの選択肢は、4番となります。
令和5年 測量士補試験 No.3 法規の中の計算問題 測量の誤差と三角形の辺の長さ(余弦定理を使って)
令和4年と令和5年のNo.3に出て来た問題も解いてみましょう。
これ、一見して、ややこしそうなのですけど、解き方の順序と、覚える公式と言葉の意味を覚えてしまうと割と簡単に出来てしまいます。

国土地理院のHPから引用
アの問題
まず、文章に出てくる最確値ですが、平均と思ってください。
この5つの測定値の平均を出します。ここで一つ注意なのですが、角度は60進法なので、60秒を超えている数字も一旦、60を足してあげます。
つまり、2つ目と4つ目のやつは、61”と65”になりますね。
で平均は、57+61+59+65+58÷5回=60”となりました。
次に、この60”と、5つそれぞれとの差はいくつあるのかを出します。これは目で見てわかりますね。
これを問題文の測定値の横にマス目を増設して書いていきましょう。
つまり、測定値と最確値の差は上から、-3、1、-1、+5、-2となります。
この差のことを、残差といいます。
最終目標の標準偏差を出すには、この残差の二乗が必要になってくるようです。
もう理屈抜きで、この公式は覚えましょう。
標準偏差=√ΣV²/n(n-1) です。
ルート、nカッコn引く1カッコ閉じ ぶんの シグマブイ二乗 です。
nは測定回数です。なので、n(nー1)は、5(5-1)で、5×4で、分母は20ですね。
Σは合計という意味の記号です。Vはさっき出した残差ですね。
残差の二乗V²の合計Σが分子になるということです。
この式に、わかっている数字をあてはめてあげると、
√(-3)²+1²+(-1)²+5²+(-2)²/20
√9+1+1+25+4/20=√2となりまして、1.4。 標準偏差は1.4となります。
イの問題
さっき平均は60”と出しましたね。これ、どんどん繰り上がって、結局測定値は、60°になるのです。
次に、例によって、図を書きましょう。
2辺とその間の角度が判っているときは、余弦定理というやつを使います。cosは、巻末の関数表から引っ張ってきます。
三角形ABCで、向かい合う辺のことをabcとしますと、
b=√a²+c²-2×a×c×cosB (右側の√を外すなら、b²=a²+c²-2×a×c×cosB)となります。これは覚えるしかありません。頑張りましょう。
☆コサインが90°をこえると関数表には載っていません。そんなときは、(180°-○○○°)として関数表を使います。
この問題では、
b=√8²+3²-2×8×3×cos60°
b=√73-48×0.5 (cos60は0.5)
b=√49=7mとなります。
なので、この問題の答えは、1番となります。
基礎数学のまとめ
この法規の中の計算問題は、基礎といいつつ、文系の人や、数学をすっかり忘れてしまった人には、気の重たい問題となります。
まずは、ラジアンと、正弦定理、余弦定理、標準偏差の公式を覚えてしまいましょう。
うろ覚えでも、実際に解いて、何回かチャレンジしていくと大丈夫になってくると思います!
測量士補試験のNo.3は計算問題の一発目なので、幸先の良いスタートを切って頂きたいと思います。
(PR)
数学に苦手意識がある、勉強時間が取れない、測量士補の先の資格を狙っているという方へ
それでもやっぱり計算問題への苦手意識が払拭できない、まとまった勉強時間が取れない、勉強の進め方が判らない
個人の置かれている環境は人それぞれですし、独学に拘ることなく、教えるプロに任せた方がベターな選択の場合があります。お金は独学より掛かってしまいますが、お金では買えない時間を有効活用できることでしょう。
東京法経学院
測量士補、その先の測量士・土地家屋調査士試験対策の老舗の資格学校として、東京法経学院があります。リアルな通学と、通信があるようですので、ご自分の環境にあったコースを検討できますね。
WEBが流行る少し前までは、測量関係の資格は、東京法経学院一択の時代があったようですね。
そういった意味では、教える手法・方法の蓄積が、難関資格試験ではモノを言いますので、老舗の安心感は大きいですよね。(PR)
アガルート
WEB講座が好評で、近年、合格者を増やしているアガルートです。スキマ時間の有効活用に特化した講義内容になっているようです。地方県に住んでいると通学はほぼ出来ませんし、仕事や家庭の役割をこなすと、まとまった時間が取れない人には、とてもマッチした講義だと思います。
すでに来年令和7年の、5月の測量士補試験、10月の土地家屋調査士試験向けの、講座があるようですね!(PR)
アガルート・初学者向け【土地家屋調査士試験】2025年(令和7年度)合格目標講座
今回の令和6年測量士補試験には出なかったのですが、ここ10年で6回も出題されてきたGNSS測量の基線解析の問題に触れておこうと思います。
そして、今まで出題されていた普通の基線解析の問題に替わって、その基線解析の中に入っているセミダイナミック補正の問題が、今年、令和6年に出題されました。
一見、難解な問題のように感じてしまいますが、慣れると手計算もそう多くないないので、解答しやすい問題だと思います。
因みに、GNSSとは、グローバル・ナビゲーション・サテライト・システムのことです。人工衛星での測量ということですね。
GNSSに関しては文章問題の方でも出てきますから、基本の用語と意味は覚えておきましょうね。
そして、計算問題においては、衛星は出てきません。立体のグラフの中のある線の長さを求める問題となります。セミダイナミック補正は地殻の変動を補正する問題になります。
令和3年 測量士補試験 No.8 GNSS測量の中の基線解析
基線解析と聞くと、何やら難しい感じがしますね。
X軸、Y軸、Z軸を、立方体の箱に見立てて、それが、縦、横、高さ、になったと思うとずいぶん気が楽になります。
で、その箱を対角線を突っ切るように、斜めの線の長さはいくつですか?と言う問題なのですね。

国土地理院HPより引用
この問題、ΔXとΔYの二つで、まず平面のベクトル(斜距離)を出して、今度はそのベクトルが底辺の三角形をΔZを高さとして作り、その三角形の斜距離を出す方法があります。
しかし、私は、公式を覚えて解いていました。なぜなら頭の中が、こんがらがってくるからです。
公式は、
√(ΔXb-ΔXc)²+(ΔYb-ΔYc)²+(ΔZb-ΔZc)²
となります。
私がそうなんですが、デルタとかのギリシア文字が付くと急に難しく感じてしまうのが、文系の人の特徴ですねw
でも、これ単に記号というか、マス目の場所を表しているだけと思えばいいのです。
表8の基線ベクトル成分のΔXの縦の2つを見て下さい。
これを数直線で表すと、AからBに+300、AからCに+100動いたということで、その差は、+200になりますよね。
この計算が、(ΔXb-ΔXc)となるのです。つまり、(+300-(+100))で+200になります。で、これの二乗ですから、この部分だけだと40000となります。
一気にΔX,ΔY,ΔZをやりますと、
√(+300-(+100))²+(+100-(-400))²+(-400-(-200))²
=√(+200)²+(+500)²+(-200)²
=√40000+250000+40000
=√330000 となりました。
で、この√330000は、√33と√10000に分けられますね。
なので、√33は関数表の平方根から5.74456、√10000は100になりまして、
5.74456×100で、
574.456mとなりました。
なので、正解は2番となります。
今年の試験ではこの良く出ていた基線解析の問題は出なかったのですが、10年中、6年も出ていますので、公式と解き方は覚えておいた方がいいですね。手での計算も楽な部類の問題ですし。
令和6年 測量士補試験 No.8 GNSS測量の中のセミダイナミック補正
令和6年の測量士補試験では、普通の基線解析の問題ではなく、セミダイナミック補正の問題が出されました。過去問では令和3年に出ていますね(令和1、令和2は文章問題でした)。

このセミダイナミック補正の問題。問題の文章が長く、表が多くて、なにやら難しそうな、面倒くさそうな第一印象ですね。でも解いてみて、慣れれば大丈夫になってきます。
まず、セミダイナミック補正とは、ある時点(2011)の電子基準点の座標値を「測量成果2011」としてまとめて、その「測量成果2011」に載っているものと、今測ったものとの差を補正するものです。これは、地球の地殻変動で日本の地面が動いていますので、どうしても誤差がでてきてしまいますね。
セミダイナミック補正は、その地殻変動の歪みの影響を補正しようとするものなのです。
あと、「元期」と「今期」という語が出てきます。元期は「測量成果2011」のときの数値で、今期は、今測ったやつの数値のことです。
このセミダイナミック補正の問題は、つまるところ、この元期と今期の、足し算か引き算の問題です。
問題文と表に書いていることを、じっくり見てみれば正解に導くことが出来ます。
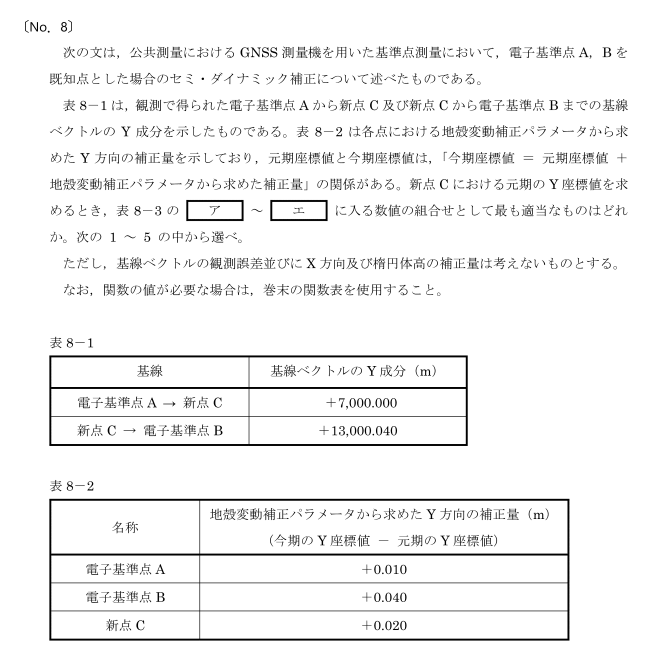
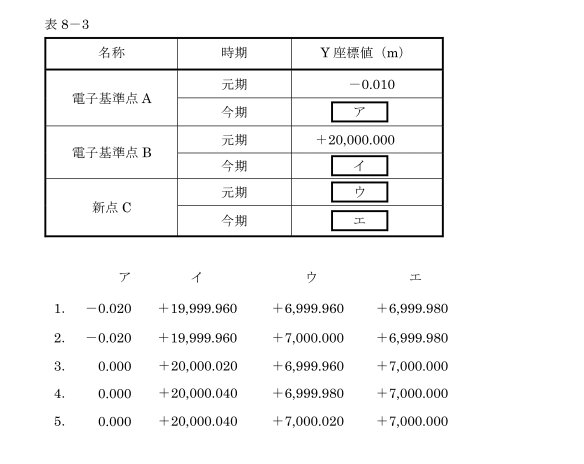
国土地理院HPより引用
問題文に「元期座標値と今期座標値は、「今期座標値=元期座標値+地殻変動補正パラメータから求めた補正量」の関係」と書いてありますね。地面が動いた分を足してやるということです。
空欄アでは、電子基準点Aの元期は、表8-3に、-0.010とあります。
表8-2の電子基準点Aの補正量は、+0.010となっています。もともとの元期が-0.010で、補正されたのが+0.010なのですから、これを相殺する形で(足し算して)、今期が、0.000になりますよね。
空欄イでは、電子基準点Bの元期は、表8-3で、+20,000.000とありまして、表8-2の電子基準点Bの補正量は、+0.040とあります。もともと20,000で、補正されたのが+0.040なのですから、+20,000.040となりますね。
ここで、
空欄アで1、2、3に絞られて、空欄イで4、5に絞られましたね。
次に、先に空欄エから見てみますと、
表8-1に、基線ベクトルのY成分は、+7,000.00と書いています。
つまり、空欄エは、今期は+7,000 となります。
空欄ウは、「今期座標値=元期座標値+地殻変動補正パラメータから求めた補正量」
の式から、「7000= X + 0.020 」となりまして、+7000-(+0.02)=+6,999.980 となります。
ですので、答えは、4番ということになりました。
令和3年のセミダイナミック補正の問題は基準点は一つだけでしたが、令和6年では2個になりました。しかし、落ち着いて読むと、単純な足し算引き算の話だったということがわかりますね。
とはいうものの、この手の問題は慣れが必要かなと思いますので、何度かチャレンジしてみて下さい。
(PR)


