今回は、測量士補試験の科目の中の多角測量に出てくる計算問題をあげてみたいと思います。
令和6年 測量士補試験 No.5 多角測量の中の高低角と高度定数の較差
まずは今年令和6年に出た問題から見てみましょう。
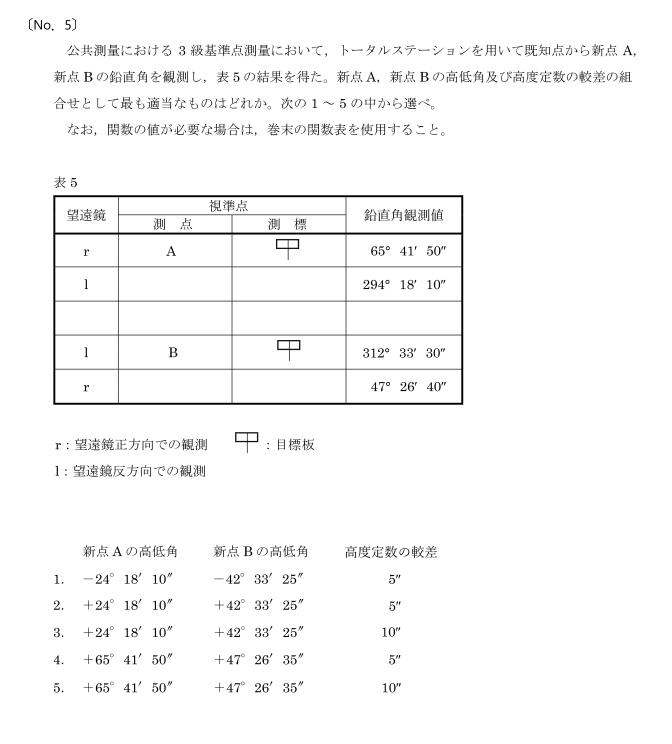
国土地理院HPより引用
始めこの問題をみたとき、「なんだこれは?」と思いました。
「緑の過去問280」にも、テキストにも載っていない問題なのです。
私は試験中はザっと見て、多少あれこれ考えましたが、後回しにしまして、
とにかく余りの時間で、360、180、の足し算や引き算をしました。
で、測点Aの鉛直角観測値を足すと、360°
測点Bの鉛直角観測値を足すと、360°00’10”
10”の差。
これが高度定数というやつの較差だなと思い、選択肢3か5に絞った次第です。
3にしたのは、選択肢5が、測点Aの鉛直角観測値と同じ数字。
こんなことは無いでしょう~と思いまして、3にして、結果的に、正解でした。
そうです。最後は当てずっぽうでしたw
私は、家に戻って、各資格学校の試験の講評を見ました。
ある資格学校の先生曰くこの手の問題は「20年くらい出ていなかったのではないか」とのこと。
どおりで過去問題集に載っていないはずです。
この問題、天頂角、高低角のことを理解していたら、とても簡単な計算問題だったようなのです。
天頂角とは、0°(てっぺん)からの角度(問題には書いてないですけど)で、90°から引いてやると残りが高低角となるようです。つまり鉛直角観測値が天頂角と同じということですね。

アガルート中山先生のブログから引用
90°と270°の水平線のラインから見て、90°と270°より上にある場合はプラス、下にある場合はマイナス。
つまり、この問題で行くと、測点Aのrの場合は、90°-65°41’50”=+24°18’10”
ℓの場合は、294°18’10”-270°=+24°18’10” と同じになります。 これがAの高低角になるわけです。
次に、測点Bのrの場合は、90°-47°26’40”=+42°33’30”
同じくBのℓの場合は、312°33’30”-270°=+42°33’30” となりました(問題文の選択肢は25”ですけど、誤差なのでしょう)。
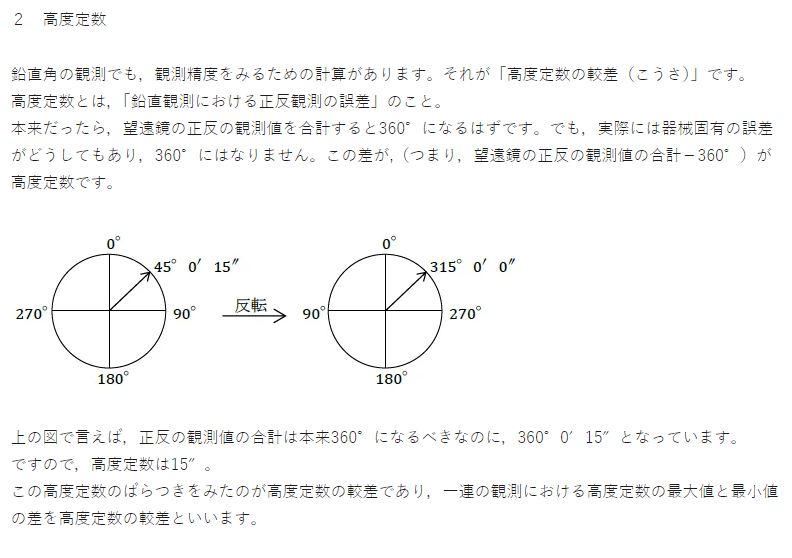
アガルート中山先生のブログより引用
そして、高度定数の較差は、測点Aのrとℓを足したのは、360°
測点Bのrとℓを足したのは、360°00’10” でその差は、10”
これが高度定数の較差ですね。
ですので、答えは、3番となりました。
この問題、用語の意味が解っていたら、計算も楽な問題でしたね。
私は知らなかったので、後回しにして、悪戦苦闘しましたけどw
ふわっとでも、用語の意味とやり方を覚えていれば、皆さんは大丈夫だと思います。
令和2年 測量士補試験 No.7 多角測量の中の高低角の観測
高低角と聞いて、よく過去問に出てきていたのは、こちらの問題ですね。
過去10年間に3回も同じような問題が出ていますので、解き方は知っておいた方が良いですね。
この問題の、理屈は簡単ですので、計算間違いをしないようにすればきっと正解できます。
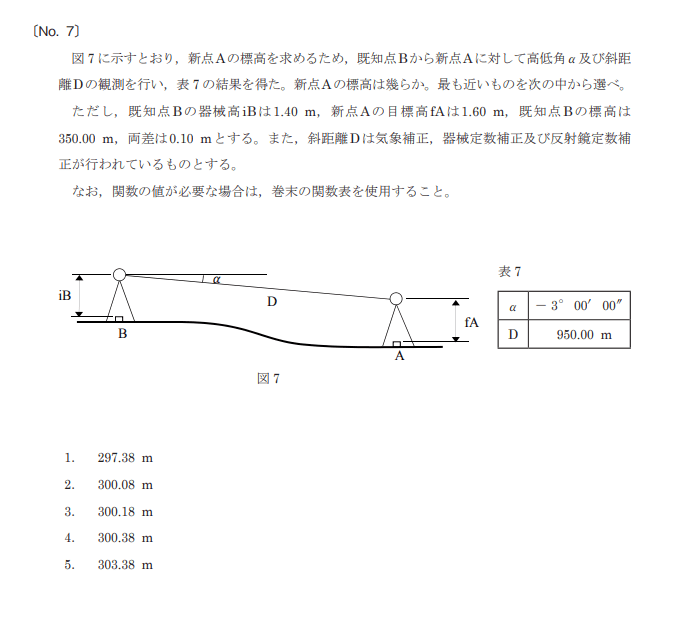
国土地理院HPより引用
ここで「両差」という語が出てきます。お相撲の技、両差し(もろざし)ではありません。
地球が丸いことによって起きる誤差を球差、大気の歪みを気差というようです。併せて、両差。
それだけで十分です。
で、この両差、問題文でいうところの、0.10は、右か左かのどっちかに足したり引いたりしないといけません。
そこで、ルールとして、既知点から新点をみるときは、既知点側に+します。
問題の図の細長い三角形の縦(高さ)をサインを使って求めますと、
斜距離950m×sin3°=950×0.05234(関数表から)=49.723m となりますね。
左の既知点Bの側を足してあげると、
標高350m+器械高1.4m+両差0.1m
これが右側の全部を足したやつと同じになるわけですね。
右側の新点Aの方は、
Aの標高(これを求める)+目標高1.6m+さっきの49.723m になります。
左と右をイコールでつないでやると、
350m+1.4m+0.1m=H(標高)+1.6m+49・723m
H(標高)=300.177m≒300.18m となりましたので、答えは3番となります。
理屈も簡単ですので、サインで高さを求めて、右と左をイコールで結べば、あとは足し算引き算です。
それと、両差を置く位置を間違わないようにしなければいけませんね。
令和6年 測量士補試験 No.6 多角測量の中の方向角と座標値の計算

国土地理院HPより引用
こちらの問題は、慣れれば文系の人にも分かりやすい問題です。
サイン、コサインで、辺の長さを出す問題の後に、座標をいじる作業があるだけですね。
☆お約束事として、方向角というのは、座標上の北から右回り(時計回り)にぐるっと回ってくる角度のことです。
この問題も、図にしてみましょう。
まず、点Aの座標を仮に(0,0)としておきます。
方向角が305°ということは、ぐるっと回って270°を越えます。
で、平面距離つまり斜距離が1000m なので、作った図の左の上に、270°ラインを底辺とした三角が出来ますよね。
角度は、305°から270°を引いて、+35°となります。
斜距離と、角度が判っていると、
サインで縦の長さ、コサインで横の長さが出ますよね。
sin35°×1000m=0.5735×1000=+573.5m これが縦の長さ つまりX座標は573.5
次に、cos35°×1000m=0.8191×1000m=819.1m となります。
この819.1mは、Y軸上を左に進みます。つまり-になりますよね。なので-819.1m
これで、現時点での点Bの座標は、(573.5、-819.1)となります。
問題文から本当は、点Aは、X上(縦)は-800m、Y上(横)は+1100mだったということです。
なので、-800mから573.5mを除いてあげると、-226.5となります。
同様に、+1100mのところから、-819.1を引いてみると、280.9となります。
ですので、答えは、4番と言うことですね。
基礎数学のところの三角関数の使い方は必ずマスターしておきましょうね。
令和3年 測量士補試験 No.6 多角測量の中の方向角の計算
こちらの方向角の計算は、ここ10年で2回出ています。
解き方は簡単ですが、60進法の足し算でうっかり計算ミスが起こりやすいので、丁寧に計算しましょう。
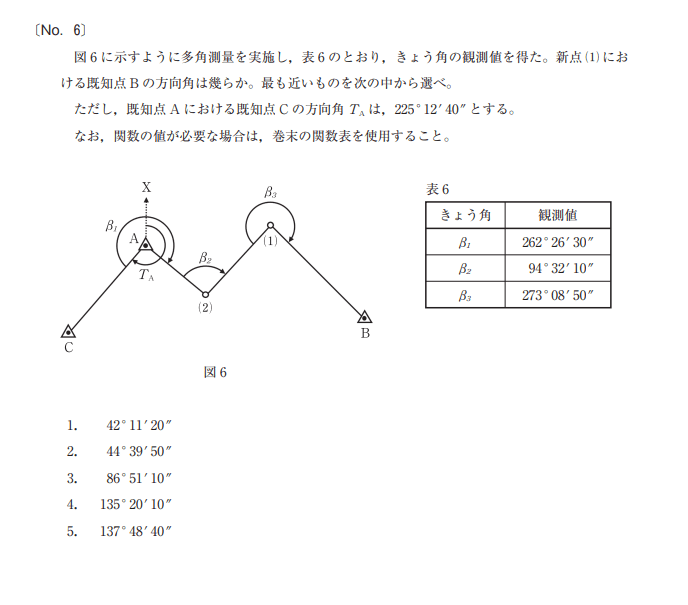
国土地理院HPより引用
方向角というのは、座標上の北から時計回りに測った角度のことでした。
まず、図に、それぞれのA点、(2)点、(1)点から北に真っすぐの線を書き入れてみましょう。
そうすると、各点の方向角がどこまでなのかが判ってきます。
で、これはもう頭に入れておくしかないのですが、覚えるととても簡単になります。
それは、ある線の方向角は、「一つ前の方向角+きょう角-180°」 となります。
きょう角は問題文に表としてありますね。
それと一個目A点だけは、そのさらに「前の方向角+きょう角-360°」 になります。
点Aは、問題文でさらに前の既知点Cの方向角は、225°12’40”とありますから、
225°12’40”+β₁262°26’30”-360°=127°39’10” となりますね(60進法で繰り上がりに注意です)
これが、A点における方向角になります。
次に、(2)ですが、方向角+きょう角-180°で計算すると、
127°39’10”+β₂94°32’10”-180°=42°11’20”となりますね。
ラスト、(1)における方向角は、
42°11’20”+273°08’50”-180°=135°20’10”
ですので、答えは4番と言うことになります。
この問題、測線を延長して、方向角を求めることもできますが、計算ミスしやすいので、この公式?でやった方が無難ですね。
肝心なのは、一個目は-360°、次からは、-180°です。
令和4年 測量士補試験 No.7 多角測量の中の偏心補正
この問題は、測量しようとした先に木があって測れないときに、ちょっとずらして三角形を作って、本来知りたかった角度を求めることです。
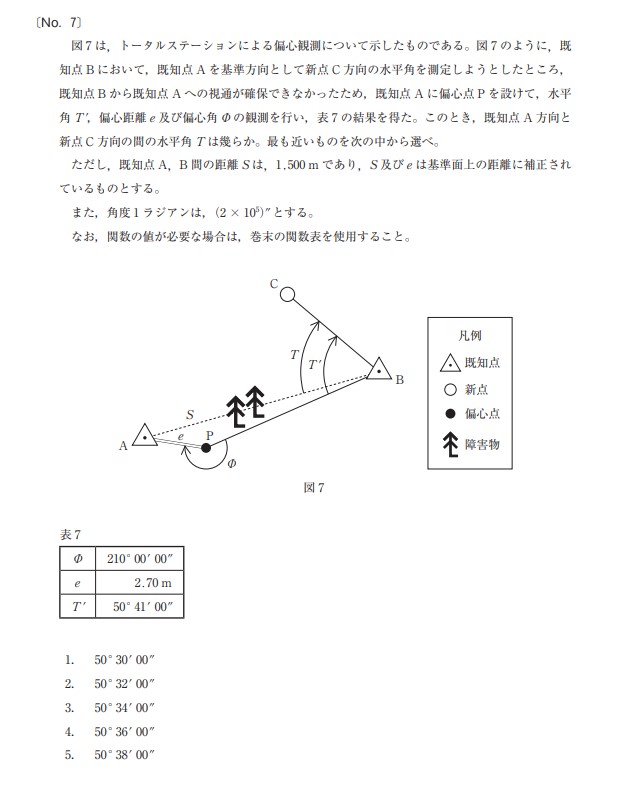
国土地理院HPより引用
ものすごく尖った針のような三角形の角度を求めることになります。
それと、これも公式でやった方が、スムーズに解いて行けます。
それは、「X秒=e/S × sinΦの内側の角度 × ρ」
サインファイ、ρはロー
ギリシア文字って分かりにくいですよね。
eは、ずらした三角形の辺
Sは、もともとの距離ですね。 ともに問題文中に与えられています。
Φは、問題文の図を見ると三角形の∠の外側ですので、この角度から内側の角度を出してあげないといけません。Φが210°なので、360°から引くと内側は150°となります。
ρは、1ラジアン=2×10⁵のことです。
これにそれぞれの数字を入れていくと、
X”=2.7m/1500m × sin150° × (2×10⁵)
sin150°は、90°を越えているので、(180-150)で、sin30°=0.5(関数表より)となりますね
これを解くと、
X”=180” となります。180”は、分に直すと、3’ですね
なので、与えられているT’の50°41’00”から、3’を引くとTになりますので、
答えは、5番の、50°38’00” となります。
数学に苦手意識がある、勉強時間が取れない、測量士補の先の資格を狙っているという方へ
それでもやっぱり計算問題への苦手意識が払拭できない、まとまった勉強時間が取れない、勉強の進め方が判らない
個人の置かれている環境は人それぞれですし、独学ではなく、教えるプロに任せた方がベターな選択の場合があります。お金は独学より掛かってしまいますが、お金では買えない時間を有効活用できることでしょう。
東京法経学院
測量士補、その先の測量士・土地家屋調査士試験対策の老舗の資格学校として、東京法経学院があります。リアルな通学と、通信があるようですので、ご自分の環境にあったコースを検討できますね。
WEBが流行る少し前までは、測量関係の資格は、東京法経学院一択の時代があったようですね。
そういった意味では、教える手法・方法の蓄積が、難関資格試験ではモノを言いますので、老舗の安心感は大きいですよね。(PR)
アガルート
WEB講座が好評で、近年、合格者を増やしているアガルートです。スキマ時間の有効活用に特化した講義内容になっているようです。地方県に住んでいると通学はほぼ出来ませんし、仕事や家庭の役割をこなすと、まとまった時間が取れない人には、とてもマッチした講義だと思います。
すでに来年令和7年の、5月の測量士補試験、10月の土地家屋調査士試験向けの、講座があるようですね!(PR)
アガルート・初学者向け【土地家屋調査士試験】2025年(令和7年度)合格目標講座
(PR)


