今回は、測量士補試験の科目の一つ、写真測量と、地図編集の緯度・経度で出される計算問題の論点を見ていくことにします。
写真測量は、飛行機やドローンなど空からの測量ということですね。
この撮影高度と縮尺は、過去10年で、8回も出た定番の問題になります。
緯度・経度の問題は、過去10年回に7回出ました。
両方とも、比の計算で解けますので、正解できるように頑張りましょう。
令和5年 測量士補試験 No.17 撮影高度と縮尺


国土地理院HPより引用
撮影高度と縮尺の問題は、問題文に図がないので、まず、とにかく、図を書くことから始まります。
図は、アガルートの中山先生のブログから引用しました。
飛行機が飛んできて、パシャリと写真を撮ったんですね。レンズの中心を境に、比になっています。

アガルート中山先生のブログより引用
この問題の画面距離7cmと、地上画素寸法20cmを、メートルに直すと、それぞれ、0.07m、0.2mとなります。
5μmのとき、0.07mなので、
0.2mのときは、何mですか? ということになりますね。
因みに、この問題では、画面の大きさ17,000画素×11,000画素は使いません。
撮影高度をHとすると、
5μm : 0.07 = 0.2 : H になります。
5μmは、5×10⁻⁶でしたね。
これを計算すると、H=0.07×0.2÷5×10⁻⁶
H=2800m となりました。
求めたいのは、標高0mからの撮影高度ですので、このHに300mを足して、3100mということになります。
答えは、5番となりました。
この撮影高度と縮尺は、測量士補試験では、頻出ですし、計算も楽な方なので、是非とも正解しておきたいですね。
令和6年 測量士補試験 No.18 オーバーラップと撮影基線長

こちらの問題は、上記の撮影高度と縮尺の問題と、重なり合わせ(オーバーラップ)の2つの話になってくるんですね。
飛行機が、パシャリ、パシャリと2回写真を撮ったときの移動距離はいくらですかと言う問題です。
その移動距離のことを、撮影基線長といいます。
ややこしそうですが、理屈と解き方を覚えてしまえば簡単な部類の問題です。

国土地理院HPより引用
フリーハンドの図で汚くて、恐縮ですが、この問題を図にするとこういうことですね。
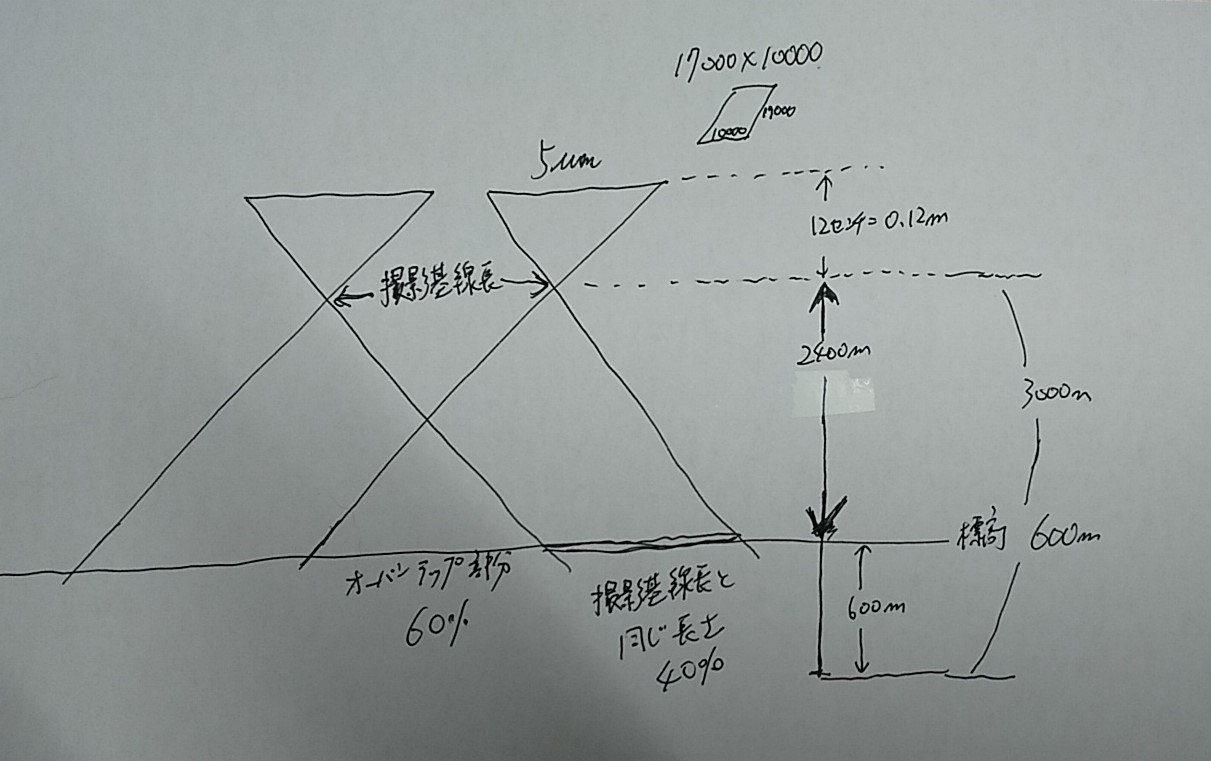
撮影基線長の図
まず、撮影高度の標高から、撮影基準面の標高を引いてあげます。なので、2400mとなりますね。
次に、比の計算で、大きな三角形の底辺の長さを出します。
5μm : 0.12 = X : 2400
X=5×10⁻⁶ × 2400 ÷ 0.12 = 0.1m となりました。
この0.1mに、本文中の「画面の短辺が」ということから、10,000画素をかけてあげると、1000mになりますね。
つまり、大きな三角形の底辺は、1000mということです。
オーバーラップが60%ですから、残りは40% つまり400m
撮影基線長と、この400mは、平行四辺形の上と下の辺なので同じ長さとなります。
ですので、答えは、1番となります。
この問題も解き方が判っていたら、小数点の移動には注意をするものの、計算は楽でしたね。
四則計算をたくさんしなければならない問題や初めて見る問題は、正解できなくても仕方がないと割り切って、解ける問題を確実にこなしていくのが良いと思います。
令和6年 測量士補試験 No.19 航空レーザー測量の欠測率
計算問題と言えば計算問題なのですが、割合を求めるもので、一回やれば、解き方が判る問題です。
令和4年にも欠測率の問題が出ましたが、「水部」を取り除く一手間がありましたが、こちらの令和6年の問題は「水部」がないので、単純に割ってあげれば回答できる問題でした。

国土地理院HPより引用
アは、水部は含まないので、1、2、3のどれかに絞られます。
b.に欠測率の式が付いていますので、そのまま計算すればOKですね。
800m×600m=480000個の格子があることになります。
点群データが無い格子が36000ということから、
36000÷480000=0.075 つまり、7.5%ということになります。
ですので、正解は、2番ということになります。
数学に苦手意識がある、勉強時間が取れない、測量士補の先の資格を狙っているという方へ
それでもやっぱり計算問題への苦手意識が払拭できない、まとまった勉強時間が取れない、勉強の進め方が判らない
個人の置かれている環境は人それぞれですし、独学に拘ることなく、教えるプロに任せた方がベターな選択の場合があります。お金は独学より掛かってしまいますが、お金では買えない時間を有効活用できることでしょう。
東京法経学院
測量士補、その先の測量士・土地家屋調査士試験対策の老舗の資格学校として、東京法経学院があります。リアルな通学と、通信があるようですので、ご自分の環境にあったコースを検討できますね。
WEBが流行る少し前までは、測量関係の資格は、東京法経学院一択の時代があったようですね。
そういった意味では、教える手法・方法の蓄積が、難関資格試験ではモノを言いますので、老舗の安心感は大きいですよね。
アガルート
WEB講座が好評で、近年、合格者を増やしているアガルートです。スキマ時間の有効活用に特化した講義内容になっているようです。地方県に住んでいると通学はほぼ出来ませんし、仕事や家庭の役割をこなすと、まとまった時間が取れない人には、とてもマッチした講義だと思います。
すでに来年令和7年の、5月の測量士補試験、10月の土地家屋調査士試験向けの、講座があるようですね!
アガルート・初学者向け【土地家屋調査士試験】2025年(令和7年度)合格目標講座
令和5年 測量士補試験 No.21 緯度と経度
今回は、測量士補試験の中の科目、地図編集の中の緯度と経度の計算問題を見ていこうと思います。
一応、計算はしますけれども、他の計算問題と毛色が違う問題となっていますね。
過去10年間に、7回も出題された頻出の問題ですので、是非とも正解しておきたい論点になります。
問題の傾向は、地図記号を読んで、その建物の緯度と経度はどれでしょうか?と言う問題になります。
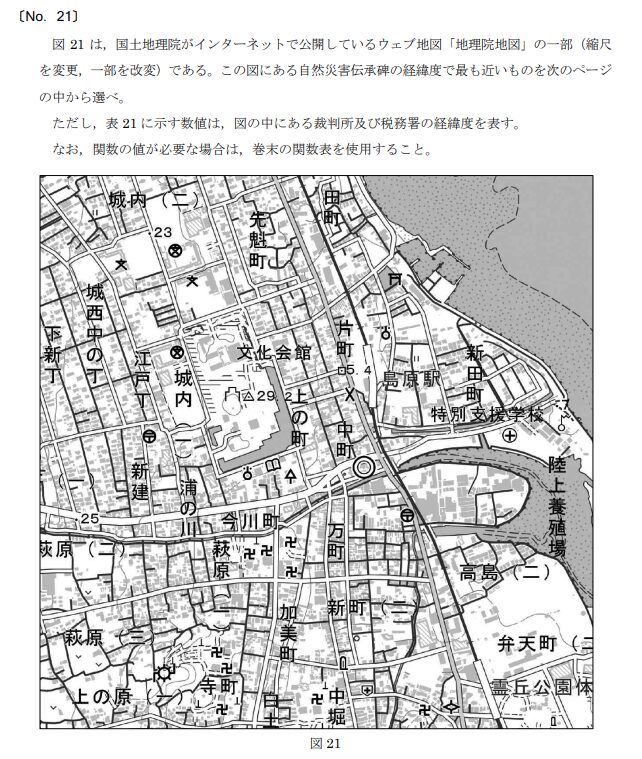
国土地理院HPより引用
この問題は、まず地図記号を選び出すことが必要になってきますので、主だった地図記号は覚えておかなければなりませんね。
国土地理院がわかりやすい地図記号のパンフレットを作ってくれています!
https://www.gsi.go.jp/common/000189126.pdf

国土地理院が出している地図記号のパンフレット
裁判所は、△の下に棒がついた傘みたいなやつです。地図の中央、お堀の下にありますね。
税務署は、◇に棒が付いたソロバンの形をしたやつになります。図の右下、駅の左にあります。
そして、自然災害伝承碑は、図の一番下の方の中央付近、中堀の中の字のやや上に、いかにも石碑みたいなマークがあります。
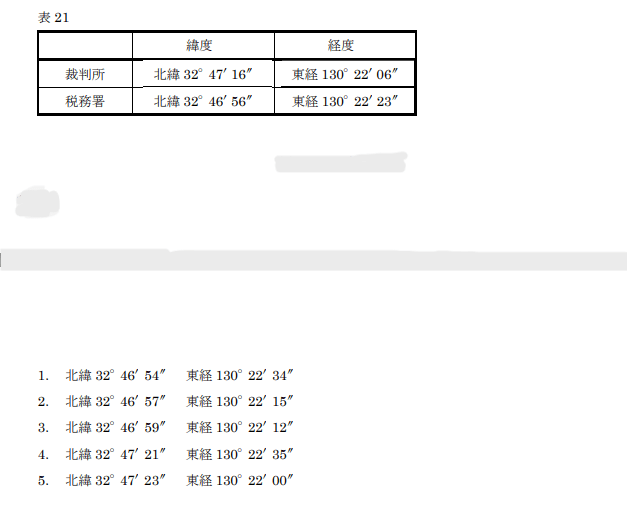
次に、この地図の余白に、裁判所と税務署の緯度経度を書き足していきます。そして、緯度経度それぞれの差を出します。
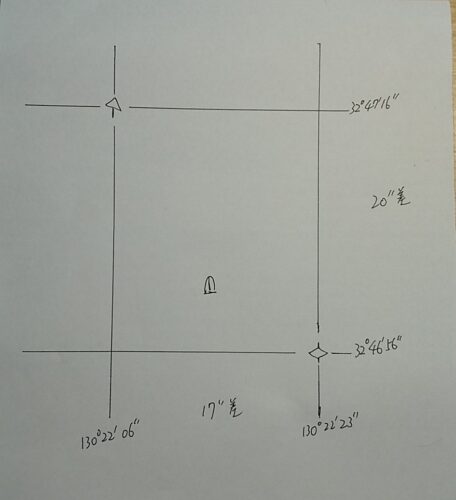
この時点で、1番と4番5番は、枠の外にありますから除外できますね。
で、伝承碑は、06”と23”の真ん中のやや左よりなので、17”を2つに割って8.5を06”に足して、真ん中を130°22’14~5”とすると、
12”の3番が怪しいですね。
念のために、比で計算してみることにします。
税務署と裁判所の地図上の緯度の差は、6.5cmとします(地図の大きさは問題文やプリントで変わりますが比なので、実際にものさしで測った数字でOKです)
税務署から伝承碑までは、1.5cmとします。
6.5 : 20” =1.5 : X
X=4.61”(この計算はアバウトです)
32°46’56”に4.61”を足すと、だいたい32°46’60”前後くらい
そうすると、やはり3番が答えということになります。
本番では、しっかり定規で測って、比で求めるので、もう少しちゃんと数字が出てくるとは思いますが、緯度経度の差を出して、その差の真ん中、1/4づつ、1/3づつとか、適当に当たりを付けても回答できる問題ですので、正解しておきたいですね。
地図編集の科目では、この緯度経度くらいしか、計算問題はありません。
そのぶん、文章題になる事柄をしっかりと覚えておきましょう。
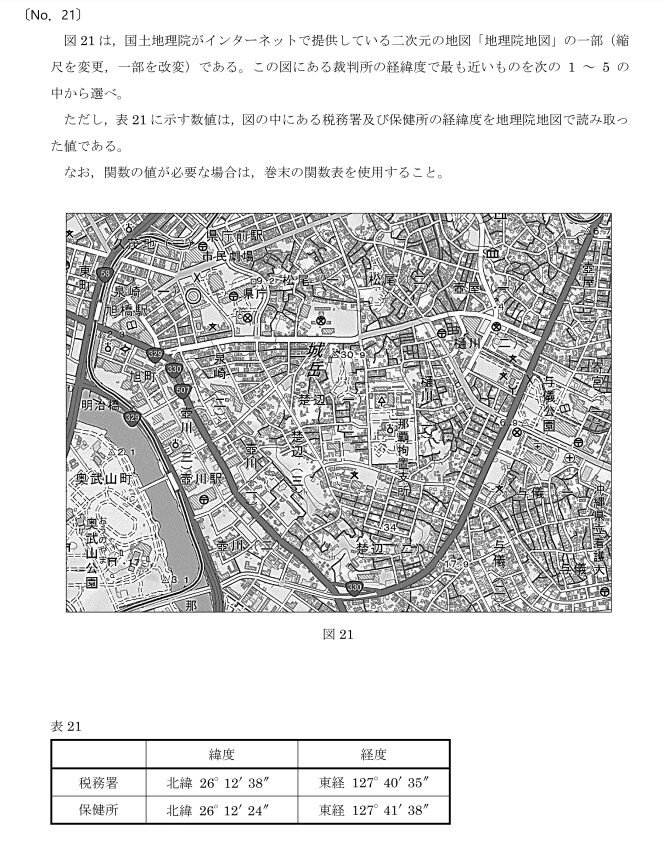
令和6年 測量士補試験 No.21 緯度と経度
令和6年緯度経度・問題

令和6年緯度経度の選択肢・国土地理院HPより引用
令和6年の緯度経度の問題は、裁判所と税務署、保健所の地図記号を見つけることからですね。
保健所の地図記号は、〇の中に+のマークになります。地図の右のやや下の方にあります。
例によって、地図に税務署と保健所の緯度経度をものさしで引いてみましょう。
つぎに、その緯度経度を書いて、差を引き算で求めます。
そうすると、緯度は、14”の差。経度は、63”の差ですね。
この時点で、選択肢1と5は、オーバーしていますから除外できます。
問題の裁判所は、127°40’35”と127°41’38”の真ん中より、やや右にあります。
差が63”でしたので、真ん中は、35”に、31.5”を足して、だいたい127°41’06”くらいになるはずです。ですので、選択肢の2も除外できそうですね。
選択肢3と4は、緯度経度ともに近いので、目分量では難しそうです。
ここで、ものさしで地図のセンチを測って、比で求める事になってきます。
経度63”が、11.8cm、127°40’35”の縦線から、裁判所までのセンチは、6.8cm
これを比で計算すると、
63:11.8=x:6.8
X≒36.3”となります。これを127°40’35”に足してやると、≒127°41’11”となりましたので、正解は、4番と言うことになります。
目分量で当たりを付けて解答できることもありましたが、選択肢の緯度経度の幅が狭い場合は、実際に地図もものさしで測ることになりますが、計算自体は簡単なので、是非ともこのNo.21は正解しておきましょう。


