今回は、測量士補試験の科目の一つ、水準測量の計算問題を見ていきたいと思います。
何度も書いて恐縮ですが、測量士補の試験問題は、文系出身の人でも、解き方を覚えたら、あとは手計算での四則計算を間違わなければ、回答できる問題がほとんどです。
始めは、公式を覚えるのがちょっと辛いかもしれませんが、それに慣れたらきっと正解していくと思います! 頑張りましょう!
令和6年 測量士補試験 No.10 レベルの設置回数
今年の測量士補試験のこちらの問題は、過去10年分の過去問題集には、載っていなかった論点の問題になります。
因みに、私はこの問題を間違えました。
選択肢2番目の、19点にして、バツとなりました。

国土地理院HPより引用
文章問題の過去問を解いていると、頻繁に出てくるのが、器械の設置回数は偶数ということ、です。
それを計算問題だからといって、すっかり忘れていました。
一回測るごとに、後視、前視と、測りますので、器械を真ん中に置いて、前後の距離で一回分ですよね。
なので、最大視準距離が45mですので、前と後ろを足して、90mが一回分となります。
1.7kmは、1700m
1700÷90=18.88 となりました。
で、わたしは、これだ!と思い、選択肢2番の19点に飛びついて、バツ。
器械の設置回数は偶数ですので、最低回数は、20点となりまして、答えは3番となります。
この問題は、計算自体は難しくなくて、測定回数の方法やお約束事をきちんと理解しているかを試す問題でしたね。
5択の中には、気が急いて、間違いを起こさせやすい数値もありますので、気を付けましょう。
令和6年 測量士補試験 No.12 標尺の補正
こちらの問題は、過去10年間で4回も出てきている頻出の問題になります。
少し長めの公式ですが、覚えてじっくり計算すれば、大丈夫な問題です。
ですので、得点源にしてしまいましょう!

国土地理院HPより引用
公式を覚えて、数字をあてはめると正解を導くことが出来ます。
まず、標尺の補正の量をΔCとします。これを出して最後に表にある観測高低差に足してやればいいのです。
あとは、問題文に出ている数値をおさらいしますと、
標尺改正数をC₀、観測時の温度をT、基準温度(=問題文中の○○℃において…のやつ)をT₀、膨張係数をα、観測高低差をΔH とします。
で、
Δc={C₀ + (T-T₀)×α }×ΔH
となります。この公式は、メモに書いて机の周りに付箋で貼ったりして、始めにがっつり記憶して、何回かチャレンジすると覚えてきます。
で、数字を入れていくと、
Δc={10µm +(28℃-20℃)× 1.5×10⁻⁶}× -50
となります。
式の中でまず出来る計算、28℃-20℃×1.5は、12になりますね。
10µmは、10×10⁻⁶で表します。
で、この10⁻⁶で、くくってあげれば、ずいぶんすっきりした式になります。
ΔC=(10×10⁻⁶ + 12×10⁻⁶)×-50 =10⁻⁶(10+12)×-50
=10⁻⁶ × 22 × -50 =10⁻⁶ × -1100
小数点が左に6個動くことですから
=-0.0011
となります。
最後に、表12の、もともとの観測高低差-50mと、この-0.0011で、-50.0011m
答えは2番ということになります。
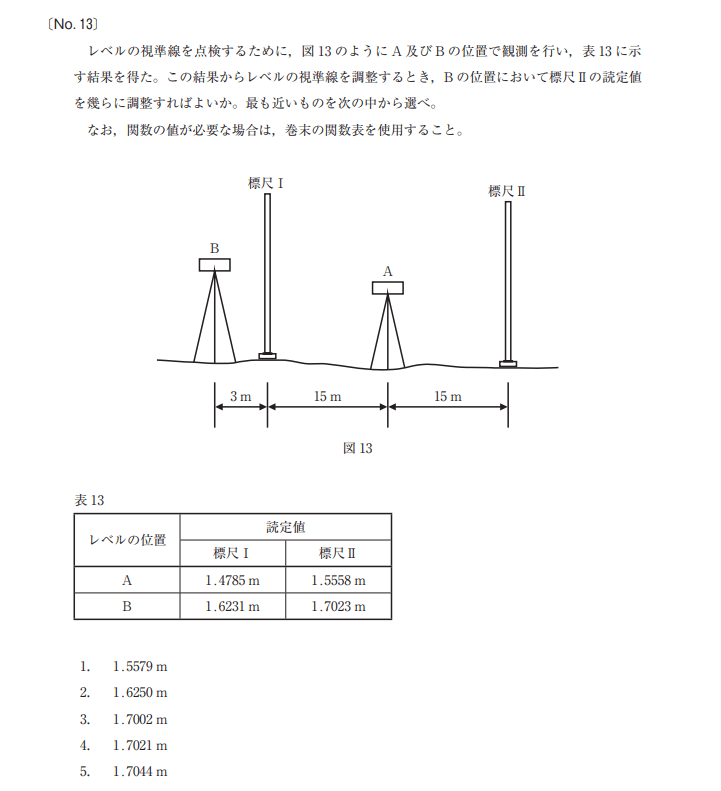
令和4年 測量士補試験 No.13 レベルの点検と調整
こちらのレベルの点検と調整の問題は、今年の令和6年の測量士補試験には、出てきませんでしたが、過去10年間で4回出てきていますので、解き方を押さえていた方が絶対に良いですね!
私は、この問題は理解するのにかなり苦労しましたが、解き方の順序を覚えてしまって、淡々と計算することで正解できるようになりました。
国土地理院HPより引用
私は最初、この問題の意味が良く分かりませんでした。視準線の誤差を調整するための作業の計算方法ということらしいですね。
で、この問題の解き方ですが、公式ではなく、順序を覚えた方が気が楽です。
まず、問題文の表をみて下さい。
レベルAが標尺の真ん中にきて、おそらく正しいとします。 レベルBは、外に外れているので誤差があるだろうと仮定して、誤りとします。因みに、同じレベルを使用しています。
次に、レベルBから見て、遠い方の標尺Ⅱから、近い方の標尺Ⅰを引いてあげるのです。
レベルAの段は、遠い1.5558-近い1.4785=0.0773 となります
レベルBの段は、遠い1.7023-近い1.6231=0.0792 となりました。
先ほど書きました、正しいと誤り。
今度は、正=レベルAの差から、誤=レベルBの差を、引いてあげるのです。
レベルAの差0.0773-レベルBの差0.0792=-0.0019 となります。
☆ここで、問題文の図の3m、15m、15mの関係性から、1.1を掛けてあげるのです。これは始めは理屈抜きで「1.1を掛けるとする」と覚えた方が楽ですね。どうやら、過去問において、1.1以外は無いようなのです。
-0.0019×1.1=-0.00209 となります。
最後に、誤りとしたレベルBで、遠い方の1.7023から、引いてあげると、
1.7023-0.00209=1.70021 となりました。
答えは、3番ということになります。
表を見て、正と誤(通常はレベルAとレベルB)。遠いから近いを引く。そして、出した数値の、正から誤を引く。
それに1.1をかける。
最後に、それを、誤の遠い方(レベルBの標尺Ⅱ)の数値から、引いたり足したりするという順序になるのです。
令和5年 測量士補試験 No.13 往復観測の較差
こちらの問題は、過去10年間に5回も出て来た、まさに頻出問題です。
やり方を順序立てて進めていくのですが、手での計算がけっこう多くて、疲れますし間違いも多くなりがちです。
ですので、落ち着いて計算を進めていくようにしましょう。

国土地理院HPより引用
まず、実際に測った往路と復路の較差を求めます。
目で見て暗算が可能ならしてみましょう。
観測区間①は、0.0004m=0.4ミリ
観測区間②は、0.0005m=0.5ミリ
観測区間③は、0.0006m=0.6ミリ
観測区間④は、0.0012m=1.2ミリ と言うことになりました。
次に格差の許容範囲を求めていきます。
問題文にある2.5㎜√Sの、Sに表の観測距離を入れますが、注意点としては、メートルをキロメートルに直して揃えてあげることですね。
この問題は幸いにも、観測距離が全部同じの250mなので、
2.5√0.25 となります。
これは、2.5√25×√0.01 となり、2.5×5×0.1となりまして、1.25㎜となりますね
許容範囲は1.25ミリですので、観測区間①②③④ともに、クリアしました。
しかし、お約束事として、全部クリアした時は、全ての区間を足したものでも一回、計算しなければなりません。実に面倒ですけど。
①②③④の観測の較差を全部足してあげます。
0.4+0.5+0.6+1.2=2.7ミリが全体の較差となりました。
この全体の許容範囲は、2.5√0.25+0.25+0.25+0.25 となり、2.5√1 つまり2.5ミリとなりますね。
なので、全体としては、許容範囲を超えてしまっているのです。
こういう場合は、①②③④の中で、一番、較差のあった④の区間を再測するという決まり事になっているのです。
ですので、答えは、3番となります。
この問題は、観測距離が全部250mでしたので、計算が少し楽でしたね。
令和3年 測量士補試験 No.13 標高の最確値
こちらの標高の最確値も過去10年間で、5回も出題されている論点になります。
解き方の手順を覚えると、得点しやすい問題ですので、計算ミスがないように頑張りましょう。

国土地理院HPより引用
最確値とは、もっとも確からしい推定の値というそのままの意味になります。
この問題は、既知点Aから新点Pは、見下ろすかたち
既知点Bから新点Pは見上げるかたち
そして、新点Pから、既知点Cを見上げる形になりますので、引き算をしてあげることになります。
Aは、標高13.339-8.123=5.216m
Bは、標高4.974+0.254=5.228m
Cは、逆に見ることになりますので、17.213-11.994=5.219m となります。
☆ここで、表ー1の観測距離の上から、2km、4km、1kmとありまして、当然距離が近いほうが、正確だろうということが言えますよね。
これを、重みというらしいのです。
で、この重みは、距離に反比例するということ。良く分からなくても、2、4、1を、ひっくり返して、まず分数の形に直してみましょう。
そうすると、1/2、1/4、1/1 となりまして、次に分母を合わせます。
2/4、1/4、4/4 となりますね。
で、この分子の部分を抜き出して、2:1:4 というかたちが、重みになるわけです。
そうして、この重みをそれぞれの標高にかけて、平均を出すということになります。
ここで計算を楽にするために、
其々の標高の数字の前の部分を計算しないように工夫します。
つまり、5.200は、3つとも同じですから、
5.2+ 0.016×2+0.028×1+0.019×4 / 2+1+4 となります。
この計算式は何度かやって慣れれば大丈夫です。重みを分子ではかけて、分母では足すのです。
これを計算すると、5.2+0.019となり、5.219 となります。
答えは、2番ということになりました。
&
数学に苦手意識がある、勉強時間が取れない、測量士補の先の資格を狙っているという方へ
それでもやっぱり計算問題への苦手意識が払拭できない、まとまった勉強時間が取れない、勉強の進め方が判らない
個人の置かれている環境は人それぞれですし、独学に拘ることなく、教えるプロに任せた方がベターな選択の場合があります。お金は独学より掛かってしまいますが、お金では買えない時間を有効活用できることでしょう。
東京法経学院
測量士補、その先の測量士・土地家屋調査士試験対策の老舗の資格学校として、東京法経学院があります。リアルな通学と、通信があるようですので、ご自分の環境にあったコースを検討できますね。
WEBが流行る少し前までは、測量関係の資格は、東京法経学院一択の時代があったようですね。
そういった意味では、教える手法・方法の蓄積が、難関資格試験ではモノを言いますので、老舗の安心感は大きいですよね。
(PR)
アガルート
WEB講座が好評で、近年、合格者を増やしているアガルートです。スキマ時間の有効活用に特化した講義内容になっているようです。地方県に住んでいると通学はほぼ出来ませんし、仕事や家庭の役割をこなすと、まとまった時間が取れない人には、とてもマッチした講義だと思います。
すでに来年令和7年の、5月の測量士補試験、10月の土地家屋調査士試験向けの、講座があるようですね!
(PR)
アガルート・初学者向け【土地家屋調査士試験】2025年(令和7年度)合格目標講座
(PR)


