今回を測量士補試験の計算問題対策シリーズのラストとして、測量士補試験の科目の一つ地形測量と応用測量の計算問題を見ていこうと思います。
これまで、①法規の中の基礎数学、②GNSS測量、③多角測量、④水準測量、⑤写真測量、⑥地図編集、
そして、今回、⑦地形測量と⑧応用測量を見ることになります。
さらに、令和6年度の測量士補試験に出題された、計算問題の12問の解説を行ったことになります。
(問3、問5、問6、問8、問10、問12、問15、問18、問19、問21、問26、問27)
例年は計算問題が10問でしたが、今年は12問。ですが、過去問と比べると、私見ですが難易度は低めだったと思います。
高校から文系コースに行った人も、数学をすっかり忘れてしまった人も、少し慣れてくれば、測量士補の合格はイケると考えています。
インターネット内の資格サイトでは、勉強時間を示しているのもバラバラです。
ですが、当然、個人のバックボーンで勉強時間は変わってきますので、あんまり気にすることはなくて、過去問の理解度で判断するのが良いと思います。
この測量士補の試験は年に一回しかありませんので、ご自分の力量と勉強時間をよく考えて、余裕をもって取り掛かることをお勧めします。
令和6年 測量士補試験 No.15 地形測量の中のTSによる等高線描画
このトータルステーションによる等高線描画の問題は、示された交点はある点から何センチのところにあるか?という問題で、過去10年で8回も出てきています。
説き方も簡単ですので、正解をゲットしたいところですね。
しかも令和6年の問題は、図にして作る三角形が一個で済んでいますので、更に手間のない問題になってラッキーでした。

国土地理院HPより引用
この問題には、図がありませんので、余白などに必ず図を書いて整理しましょう。
基準点Aが標高40.8m、そのライン上の交点が標高45mと問題にありますから、このラインは上向きに6°で昇っていることがわかります。
なので、点Aから、点Bまでの斜距離50mは、登り坂ということになりますね。
では、その三角形をだいたいで書いてみましょう。
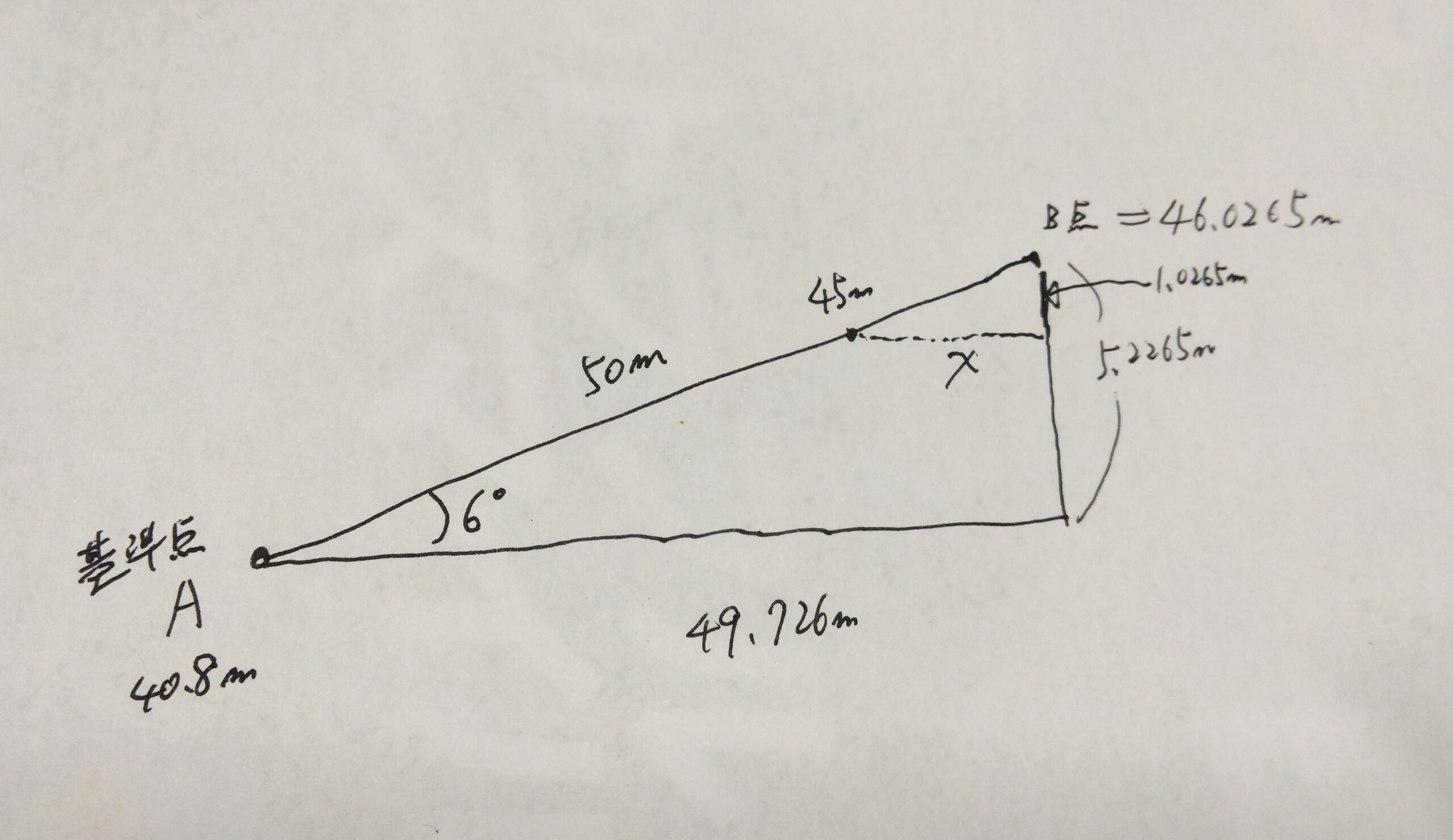
斜距離50mと高低角6度が判っていますから、サインを使ったら、B点の高さが分かります。
sin6°×50m=0.10453×50=5.2265m となります。つまりB点の標高は、40.8m+5.2265mで、=46.0265mとなりました。
次にこの三角形の底辺は、コサインで求まりますね。
cos6°×50m=0.99452×50mで、49.726m となります。
これで、比の計算で、標高45mの交点のラインの長さが求めることができそうです。
問題となっている45mの点と高さ46.0265の差は、1.0265≒1mです。
1:X=5.225:49.725
X=9.5167mとなりました。
問題で求められているのは、A点から何センチとありますので、まず、
49.725-9.5167しますと、40.20mとなります。
そして問題文に、縮尺が1/1000とありますから、
この1/1000を掛けますと、0.0402mとなります。つまり、4センチですね。
ですので、答えは、3番となります。
測量の基礎数学で覚えるサインとコサインを使う問題でした。これらは、基礎数学以外の科目でも問われますので、必ずマスターして得点源にしましょうね。
令和4年 測量士補試験 No.15 地形測量の中の細部測量
こちらの地形測量の中の細部測量は、過去10年間で、4回も出題されています。
解答の選択肢を見るとわかるように、120m先のわずかな水平誤差を計算で求めるのです。

国土地理院のHPより引用
この問題のミソの部分は、針の様に細い三角形の一辺を求めるのですが、その一辺は、実は円弧の一部ですから本当は微妙にカーブしているはずなのですが、余りに距離もないので、直線と考えるのです。
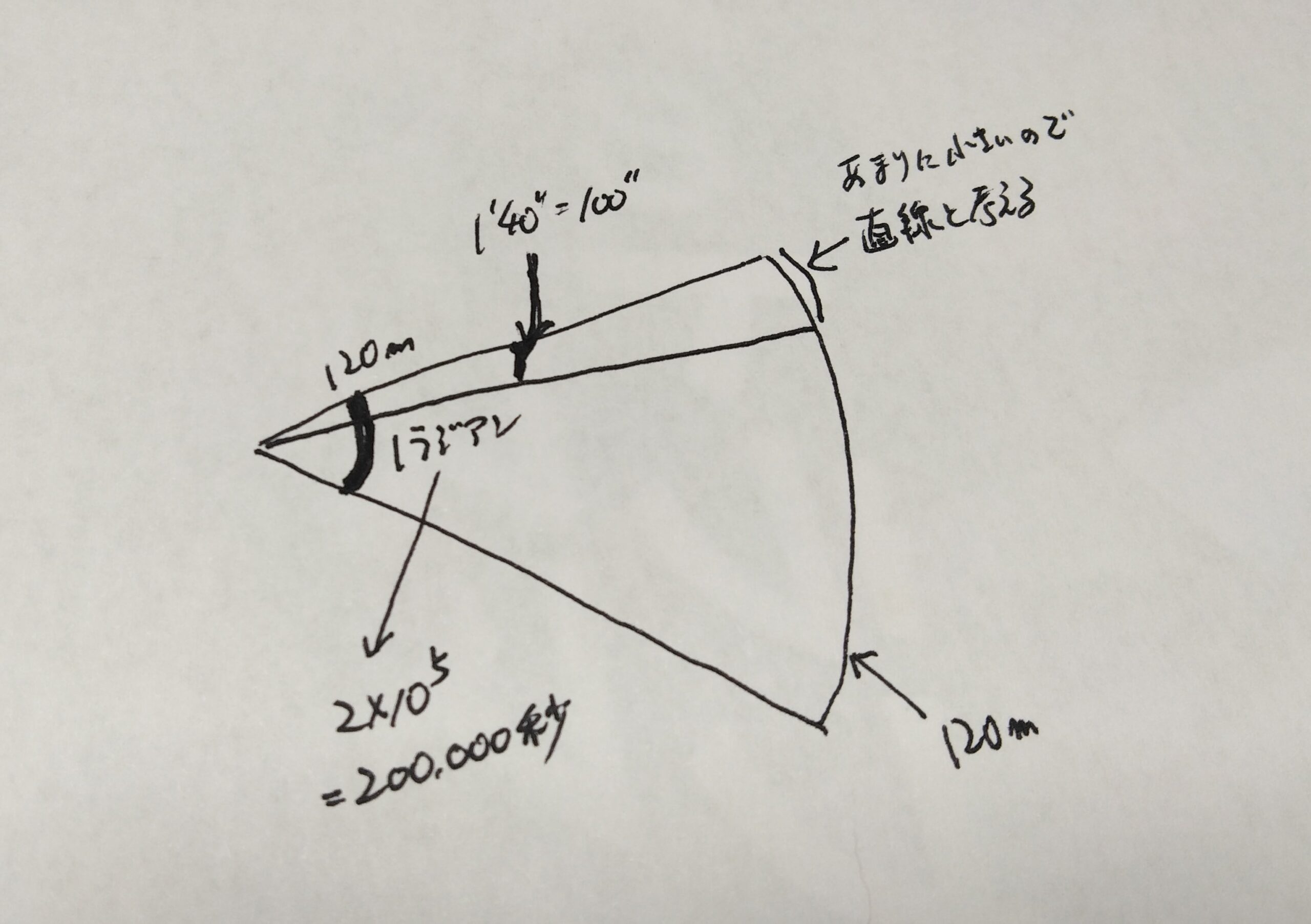
まず、点Bでの誤差は、1’40”ということですが、これを秒に直しますと、100”になりますね。
そしてこの問題は1ラジアンとの比で計算できます。1ラジアンは半径と同じ長さの円弧ですので、本問の場合は120mです。そして、2×10⁵は、200,000秒ですね。
比にしますと、
120m:X=200000”:100”
X=0.06m=6cm=60mm ということになりました。
120mの距離を測っているときの、わずか60ミリのズレなので、ほんとは、ほぼ直線に近い三角形の話なんですよね。
で、答えは、4番ということになります。
解き方さえ知れば、計算問題の中では、簡単な部類の問題ですから、確実に得点できるようにしましょう。
令和2年 測量士補試験 No.16 地形測量の中の数値地形図データ
数値地形モデルというものを作ったけど、本当は実測値と比べてどうなんだろうかという問題ですね。なので、現地の数値と、数値地形モデルの差を調べることになります。
この問題は、令和1年から3年連続で出題されていますね。今後も出される可能性はありますので解き方を知っておきましょう。
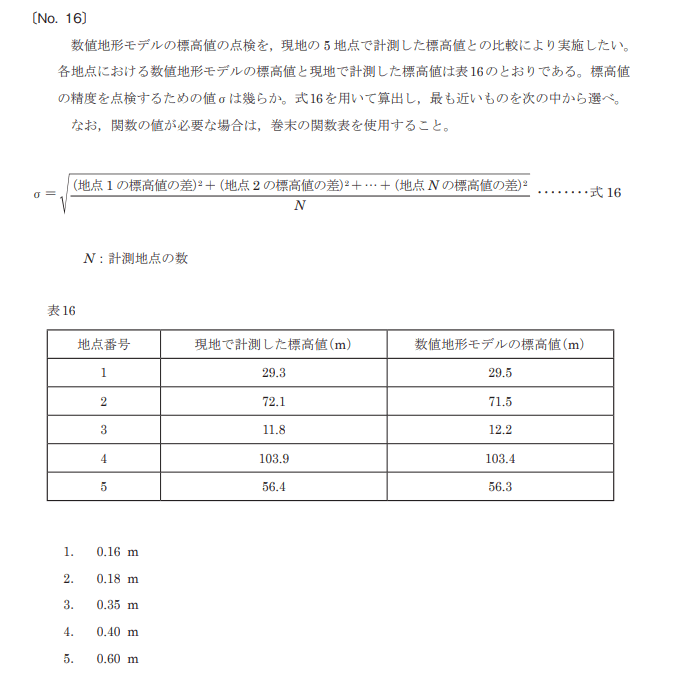
国土地理院HPより引用
式が与えられていますので、問題文をよく読んで、引き算を間違わないことです。そして、この問題は結局、ルートの計算と関数表の左側の平方根の表を駆使していきます。
最後は小数点以下4桁くらいの手計算になりますので、丁寧に計算していきましょう。
まず、今現地で測った標高値から数値地形モデルの値を引きますと(暗算でも出来そうです)、
地点番号1は-0.2、2は0.6、3は-0.4、4は0.5、5は0.1 となりました。
問題の式16では、これを二乗するものを√の中で足していくようです。なので、
上から、0.04、0.36、0.16、0.25、0.01 となりますよね。これを合計すると0.82となり、これが√の中の分子になるわけです。
分母は測った回数ですから、5になります。
σ(シグマ)=√0.82/ 5 となりますね。
このままだと、計算できないですし、関数表も使えないので変型させますと
ルートの中の分母・分子にそれぞれ100を掛けますと、√82/500 となりました。
√82/√500=√82/√5×√100、√100は10に直せますから=√82/√5×10となり、
√82と√5は、関数表の平方根から数字を引いてきて、それそれ9.05539と2.23607
あとは、手計算で(これが面倒くさい)、0.40が出てきました。
因みにコレ、小数点2位以下をバッサリ切っても0.40は出てきます。
9.0/2.2×10=0.409
選択肢の数値の幅が広い時は、計算を省略できそうなときもありますから、まず選択肢の数字の幅を確認するのもいいかもです。
で、答えは、4番となります。
数学に苦手意識がある、勉強時間が取れない、測量士補の先の資格を狙っているという方へ
それでもやっぱり計算問題への苦手意識が払拭できない、まとまった勉強時間が取れない、勉強の進め方が判らない
個人の置かれている環境は人それぞれですし、独学に拘ることなく、教えるプロに任せた方がベターな選択の場合があります。お金は独学より掛かってしまいますが、お金では買えない時間を有効活用できることでしょう。
東京法経学院
測量士補、その先の測量士・土地家屋調査士試験対策の老舗の資格学校として、東京法経学院があります。リアルな通学と、通信があるようですので、ご自分の環境にあったコースを検討できますね。
WEBが流行る少し前までは、測量関係の資格は、東京法経学院一択の時代があったようですね。
そういった意味では、教える手法・方法の蓄積が、難関資格試験ではモノを言いますので、老舗の安心感は大きいですよね。
アガルート
WEB講座が好評で、近年、合格者を増やしているアガルートです。スキマ時間の有効活用に特化した講義内容になっているようです。地方県に住んでいると通学はほぼ出来ませんし、仕事や家庭の役割をこなすと、まとまった時間が取れない人には、とてもマッチした講義だと思います。
すでに来年令和7年の、5月の測量士補試験、10月の土地家屋調査士試験向けの、講座があるようですね!
(PR)アガルート・初学者向け【土地家屋調査士試験】2025年(令和7年度)合格目標講座
ここから、ラスト8つめの科目、応用測量の計算問題を見ていきたいと思います。
令和6年 測量士補試験 No.26 応用測量の中の路線測量(曲線設置)
応用測量の中の、路線測量(曲線設置)と、次の問題のNo.27の用地測量(面積の計算)は、だいたい定位置で毎年出されています。
計算は、慣れるまで大変ですが、文系出身の人も、この2つを得点源に出来る問題にしてしまいましょう。

測量士補試験では定番の、円弧を含めた道路の長さはいくらになりますか?という問題です。
なんと過去10年中、10問の計算問題。そして、令和6年にも出題されました。
一見、ややこしそうですが、簡単な公式を2つ覚えて、数字を代入したら正解できますので頑張りましょう。
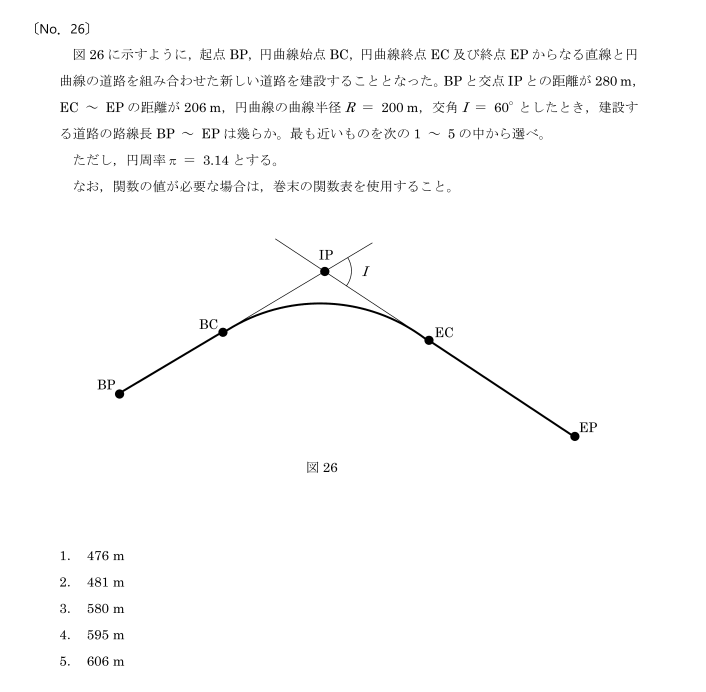
国土地理院HPより引用
まず、BCからECは円弧ですから、円の一部。なので、BC、ECから、線を下にひいて、円の中心で繋がるようにしましょう。
半径は200mとあります。
ここで、IP、つまり交角のことですが、60°とありますね。この交角の性質として、先ほど結んだ円の中心の角度と同じになります。
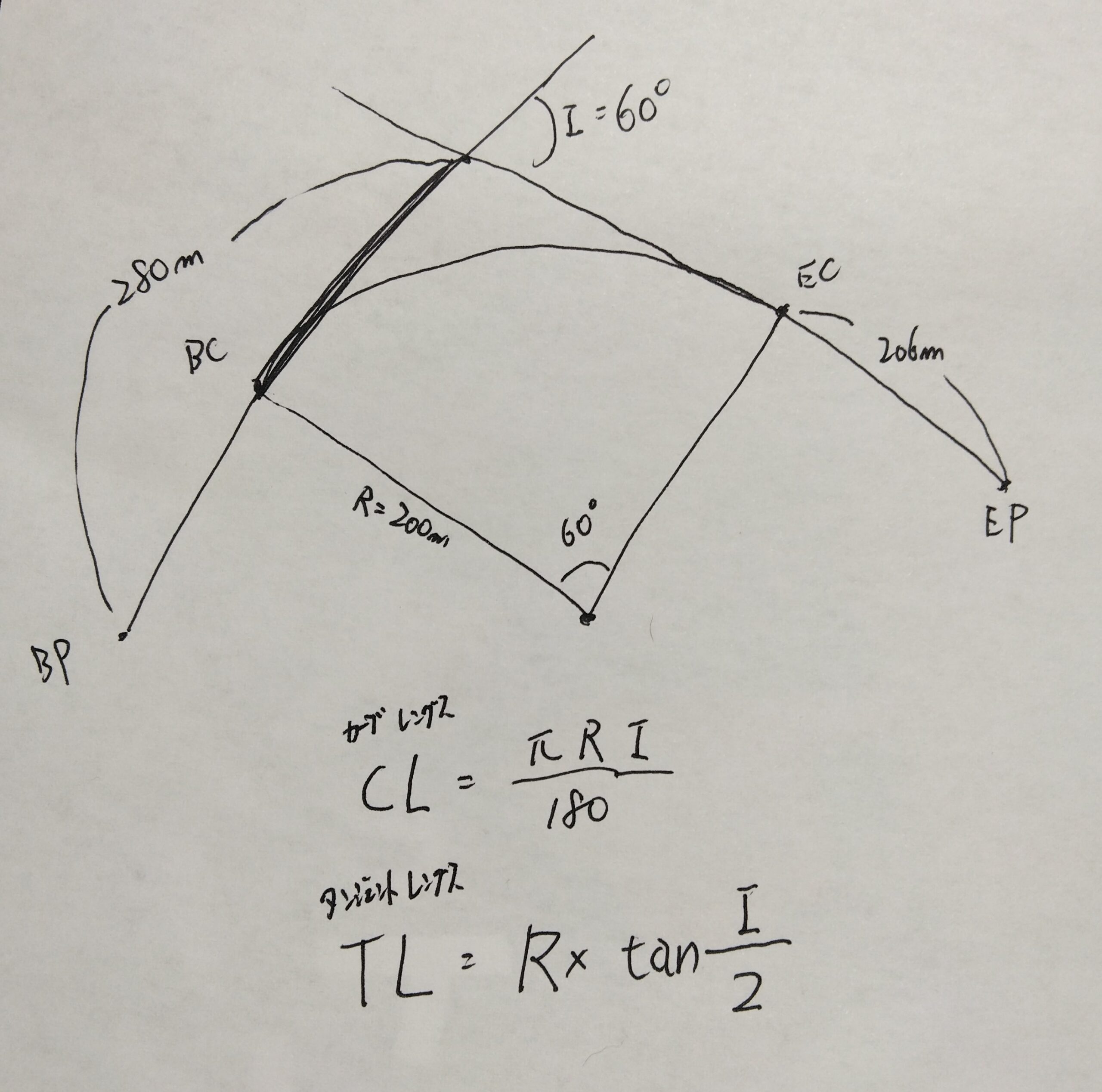
つまり、半径200m、角度は60°の扇形になるわけです。
ここで、カーブレングス・CL=π×R×I/180
という公式を覚えておきましょう。これは、直径(=2×半径)×3.14÷ 中心角/360
と同じことをいっています。
数字を代入すると、CL=3.14×200×60/180=209.33m
次に、BPからIPの長さが、280mで、今回、BC~IPの長さが要らないことになります。
この長さは、ちょうど、タンジェントレングス=TLと言われるもので、
「 R × tanI/2 」 で表すことかできます。
今回の場合は、200m×tan60/2
となりまして、tan60/2はtan30ですから、関数表から0.5773、
200×0.5773=115.46mとなりました。なので、BP~IPの280mから引いてあげると、
280-115.46=164.54mがBP~BCの長さになります。
そして、164.54+209.33+206=579.87m≒580m
答えは、3番となりました。
TL=R×tan I/2 は、結構使いますので、必ず覚えておきましょう。
令和6年 測量士補試験 No.27 応用測量の中の用地測量(面積計算)
応用測量の中の用地測量も問題ナンバー27で必ず出ている問題になります。
過去10年間、先ほどの円弧の長さの問題と、こちらの面積の計算は、必ず出ていましたし、令和6年にも出されましたので、解き方をマスターするしかありませんね!
この面積計算は、座標法、もしくは、大きな四角形で該当する4角形の回りで囲んで、出来る三角形や台形を引いて求めることになります。
足し算引き算のときに計算ミスが起きやすいので、注意しましょう。
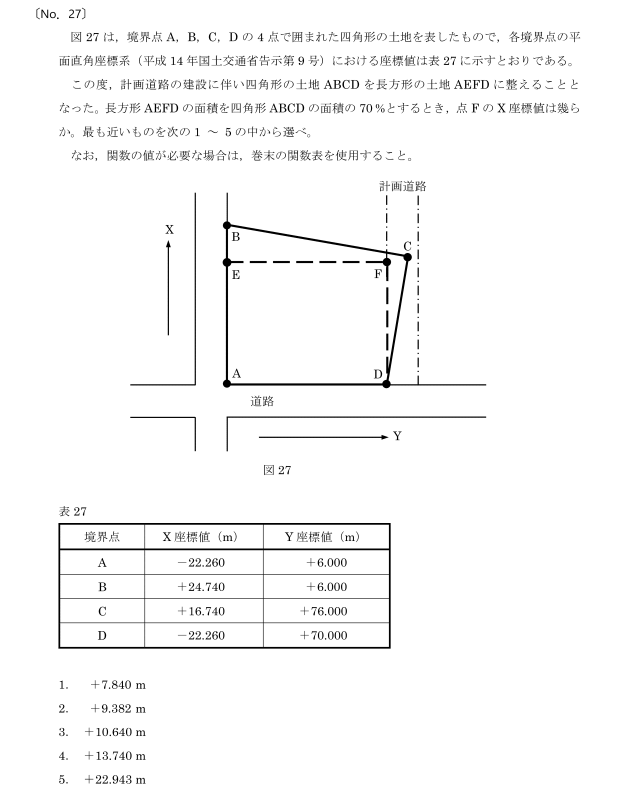
国土地理院HPより引用
大きな四角形を作って、四角形ABCDを囲って出来る三角形を引いていくやり方もありますが、
座標法というやり方を覚えれば、計算ミスを減らせることがあります。
問題を作る側も、表に出されている座標値を仮に置いてずらしてあげると、もっと簡単にできるように、数字を作ってくれていますので。
まず、X座標値の境界点Aは-22.260、このまま計算もできるのですが、かなりめんどくさいことになりそうです。なので、これを仮に「0」とします。つまり、BCD点それぞれにも、22.260を足してあげる訳です。
B点は47、C点は39、D点は0 となりました。かなりスッキリしましたね。
同じくY座標値も、+6.000を、仮に「0」としますと、
B点は0、C点は70、D点は64 となります。
座標法は、Y座標値において、後続の点から一個前の点の数字を引いたものに、X座標の値を掛けるものです。
今回の場合、A点とD点はX座標が0なので、計算しなくてよくなりました!
B点は、47(70-0)=3290
C点は、39(64-0)=2496
これらの合計は、5786となります。ここでお約束なのですけど、この5786は倍面積といって、必ず2で割ってあげないといけません。
ですので、この四角形ABCDの面積は、5786÷2=2893m²となります。
問題文の長方形AEDFは、四角形ABCDの70%の面積だそうですから、
2893×0.7をして、≒2025.1m²と出ますね。
ここで、表27を見ると、A点は+6、D点は+70で、同じ線の上にあります。
つまり、直線ADの長さは、64ということになりますね。
さっき出した長方形AEFDの面積は2025でしたから、
直線FDの長さ × 64 =2025.1 となります。
そして、直線FDの長さは、31.642mとなるわけですね。
で、一番初めに、縦のX座標は、仮に-22.260を0としておきましたが、本当は-22.260
ですから、31.642と-22.260の差が、9.382 となりました。
よって、答えは、2番となります。
座標法のお約束事を過去問を解きながら覚えていくようにしましょう。計算が多いので疲れますが、丁寧にすれば、きっと正解するはずです。
測量士補試験の各科目の計算問題についてのまとめ
ここまで、測量士補試験のそれぞれの科目で頻出の計算問題を見てきました。
文系出身者で、全問正解はしんどいことだと思いますが、解けそうな問題=相性の良い問題を見つけて、半分以上正解できれば、おそらく、この試験に勝てると思います。
私は、過去の試験で、たくさん出されている問題から、公式を覚えて、問題に慣れることをやりました。
テキストや問題集を頭から順番に覚えていかなくても、たくさん出た問題、相性の良い問題の解き方に先に触れておくのも、この測量士補試験では、有効な攻略法だと思います(あとで、その該当する箇所をテキストで復習するとなお良いですね!)。
測量士補試験は、年に一回の試験ですから、申し込みをきちんとして、5月の試験には合格されるよう、頑張っていただきたいと思います!
(PR)


